Что такое линейное преобразование

Линейные преобразования

Ортогональные преобразования.

Ортогональными называются такие преобразования плоскости, которые не меняют расстояния между любыми двумя точками, то есть преобразования \(f\) ортогональное, если для любых точек \(A\) и \(B\) выполнено \(|AB|=|f(A)f(B)|\).

Основными примерами ортогональных преобразований служат параллельный перенос, поворот и осевая симметрия.

Получим координатную запись ортогонального преобразования в декартовой прямоугольной системе координат \(O, \boldsymbol_<1>, \boldsymbol_<2>\). Обозначим через \(A\) и \(B\) концы базисных векторов: \(\boldsymbol_<1>=\overrightarrow\), \(\boldsymbol_<2>=\overrightarrow\) (рис. 12.1). При ортогональном преобразовании равнобедренный прямоугольный треугольник \(OAB\) перейдет в равный ему треугольник \(O^<*>A^<*>B^<*>\). Рассмотрим произвольную точку \(M(x, y)\). Она перейдет в точку \(M^<*>\) с координатами \((x^<*>, y^<*>)\). Нам надо выразить \((x^<*>, y^<*>)\) через \((x, y)\).

Рис. 12.1. Ортогональное преобразование.

По определению координат \(\overrightarrow=x\overrightarrow+y\overrightarrow\). Отсюда следует, что \(\overrightarrowM^<*>>=x\overrightarrowA^<*>>+y\overrightarrowB^<*>>\). Действительно, векторы \(\overrightarrowA^<*>>\) и \(\overrightarrowB^<*>>\) взаимно перпендикулярны и по длине равны 1, а потому компоненты \(\overrightarrowM^<*>>\) по этим векторам равны его скалярным проекциям на них. Эти проекции равны проекциям \(\overrightarrow\) на \(\boldsymbol_<1>, \boldsymbol_<2>\), что видно из равенства соответствующих треугольников. Теперь мы можем написать
$$
\overrightarrow>=\overrightarrow>+\overrightarrowM^<*>>=\overrightarrow>+x\overrightarrowA^<*>>+y\overrightarrowB^<*>>.\label
$$

Обозначим через \(\varphi\) угол между \(\overrightarrowA^<*>>\) и \(\boldsymbol_<1>\). Поскольку \(|\overrightarrowA^<*>>|=1\), координаты этого вектора в базисе \(\boldsymbol_<1>, \boldsymbol_<2>\) равны \((\cos \varphi, \sin \varphi)\). Тогда перпендикулярный вектор единичной длины \(\overrightarrowB^<*>>\) имеет координаты (\(\mp \sin,\ \pm \cos\)), причем верхние знаки берутся в том случае, когда пара векторов \(\overrightarrowA^<*>>\) и \(\overrightarrowB^<*>>\) ориентирована так же, как \(\boldsymbol_<1>, \boldsymbol_<2>\). Координаты точки \(O^<*>\) обозначим через \((c_<1>, c_<2>)\).

Теперь мы можем разложить все члены равенства \eqref по базису:
$$
\begin
& x^<*>=x \cos \varphi \mp y \sin \varphi+c_<1>,\\
& y^<*>=x \sin \varphi \pm y \cos \varphi+c_<2>.
\end\label
$$

Итак, мы доказали следующее утверждение.

Произвольное ортогональное преобразование в декартовой прямоугольной системе координат записывается формулами \eqref, где \(\varphi\) — угол, на который поворачивается первый базисный вектор, a \(c_<1>\) и \(c_<2>\) — координаты образа начала координат. При этом выбираются верхние знаки, если образы базисных векторов ориентированы так же, как и сами эти векторы, и нижние знаки в противоположном случае.

Параллельный перенос на вектор с сопоставляет точке \(M\) с координатами \((x, y)\) в некоторой декартовой системе координат точку \(M^<*>\) с координатами
$$
x^<*>=x+c_<1>,\ y^<*>=y+c_<2>,\nonumber
$$
где \(c_<1>\) и \(c_<2>\) — координаты \(c\).

Напишем уравнения поворота плоскости на угол \(\varphi\) вокруг некоторой точки, приняв эту точку за начало декартовой прямоугольной системы координат. В этом случае \(O=O^<*>\) и, следовательно, \(c_<1>=c_<2>=0\). Должны быть выбраны верхние знаки. Итак
$$
x^<*>=x \cos<\varphi>-y \sin<\varphi>,\ y^<*>=x \sin<\varphi>+y \cos<\varphi>,\nonumber
$$

Рассмотрим осевую симметрию относительно некоторой прямой. Примем ось симметрии за ось абсцисс декартовой прямоугольной системы координат. Тогда точка \(M(x, y)\) переходит в точку \(M^<*>\) с координатами
$$
x^<*>=x,\ y^<*>=-y.\nonumber
$$
Здесь \(c_<1>=c_<2>=0\) и \(\varphi=0\) при нижних знаках в формулах \eqref.

Определение линейных преобразований.

Основным объектом для нас будет более широкий класс преобразований, включающий в себя ортогональные преобразования.

Преобразование \(f\) плоскости \(P\) называется линейным, если на \(P\) существует такая декартова система координат, в которой \(f\) может быть записано формулами
$$
\begin
& x^<*>=a_<1>x+b_<1>y+c_<1>,\\
& y^<*>=a_<2>x+b_<2>y+c_<2>.
\end\label
$$
Взаимно однозначное линейное преобразование называется аффинным преобразованием.

Подчеркнем, что в определении линейного преобразования, вовсе не требуется, чтобы коэффициенты в формулах \eqref не обращались в нуль одновременно. Они могут быть любыми. Докажем следующее утверждение.

Для того чтобы преобразование, задаваемое формулами \eqref, было взаимно однозначным, необходимо и достаточно,
$$
\begin
a_<1>& b_<1>\\
a_<2>& b_<2>
\end \neq 0.\label
$$

Таким образом, аффинное преобразование определяется формулами \eqref при условии \eqref.

Наше утверждение вытекает по существу из утверждения о существовании решения системы линейных уравнений. Нам нужно узнать, при каком условии каждая точка плоскости имеет единственный прообраз. Формулы \eqref связывают координаты \((x^<*>, y^<*>)\) точки \(M^<*>\) и координаты \((x, y)\) ее прообраза. Их можно рассматривать как систему линейных уравнений для нахождения \(x\) и \(y\), и эта система имеет единственное решение при любых свободных членах \(x^<*>-c_<1>\) и \(y^<*>-c_<2>\) (а значит, при любых \(x^<*>\) и \(y^<*>\)) тогда и только тогда, когда выполнено условие \eqref.

Как видно из доказанного утверждения, ортогональные преобразования являются линейными. Проверка условия \eqref показывает, что они аффинные. Рассмотрим другие примеры.

Рассмотрим сжатие к прямой и примем эту прямую за ось абсцисс декартовой прямоугольной системы координат. Легко видеть, что в такой системе координат сжатие с коэффициентом \(\lambda\) записывается формулами
$$
x^<*>=x,\ y^<*>=\lambda y.\nonumber
$$
Сжатие к прямой — аффинное преобразование.

Проектирование на прямую в такой декартовой прямоугольной системе координат, для которой эта прямая — ось абсцисс, записывается формулами
$$
x^<*>=x,\ y^<*>=0.\nonumber
$$
Это — линейное, но не аффинное преобразование.

Для записи уравнений гомотетии не существенно, чтобы система координат была прямоугольной, но уравнения проще, если начало координат поместить в центр гомотетии. По определению гомотетии с коэффициентом \(\lambda\) вектор \(\overrightarrow\) переходит в вектор \(\overrightarrow>=\lambda\overrightarrow\). Если \(O\) — начало координат, координаты точек \(M\) и \(M^<*>\) будут связаны равенствами
$$
x^<*>=\lambda x,\ y^<*>=\lambda y.\nonumber
$$
Гомотетия — аффинное преобразование.

Преобразование, сопоставляющее каждой точке плоскости одну и ту же точку \(C\), записывается формулами \(x^<*>=c_<1>\), \(y^<*>=c_<2>\), где \(c_<1>\) и \(c_<2>\) — координаты точки \(C\). Оно линейное, но не аффинное.

Определение аффинного преобразования содержит упоминание о некоторой определенной системе координат, и заранее не известно, будет ли преобразование записываться формулами вида \eqref в какой-либо другой системе координат. Давайте докажем следующее утверждение.

В любой декартовой системе координат, линейное преобразование задается формулами вида \eqref, то есть:
$$
\begin
& x^<*>=a_<1>x+b_<1>y+c_<1>,\\
& y^<*>=a_<2>x+b_<2>y+c_<2>.
\end\nonumber
$$

Пусть преобразование задано равенствами \eqref в системе координат \(O, \boldsymbol_<1>, \boldsymbol_<2>\). Перейдем к системе координат \(O’, \boldsymbol’_<1>, \boldsymbol’_<2>\). Как мы знаем, старые координаты точки \(M(x, y)\) выражаются через новые координаты \((x’, y’)\) по следующим формулам:
$$
x=\alpha_<1>x’+\beta_<1>y’+\gamma_<1>,\ y=\alpha_<2>x’+\beta_<2>y’+\gamma_<2>.\label
$$
Для образа \(M^<*>\) точки \(M\) нам нужно будет, наоборот, выразить новые координаты \((x’^<*>, y’^<*>)\) через его старые координаты \((x^<*>, y^<*>)\). Они выражаются такими же формулами, разумеется, с другими коэффициентами:
$$
x’^<*>=\lambda_<1>(x^<*>)+\mu_<1>y^<*>+\nu_<1>,\ y’^<*>=\lambda_<2>x^<*>+\mu_<2>y^<*>+\nu_<2>.\label
$$

Нам требуется найти выражение новых координат \((x’^<*>, y’^<*>)\) точки \(M^<*>\) через новые координаты \((x’, y’)\) точки \(M\). С этой целью подставим в равенства \eqref значения \(x^<*>\) и \(y^<*>\) из формул \eqref:
$$
\begin
& x’^<*>=\lambda_<1>(a_<1>x+b_<1>y+c_<1>)+\mu_<1>(a_<2>x+b_<2>y+c_<2>)+\nu_<1>,\\
& y’^<*>=\lambda_<2>(a_<1>x+b_<1>y+c_<1>)+\mu_<2>(a_<2>x+b_<2>y+c_<2>)+\nu_<2>.
\end\nonumber
$$

Для нас важно, что правые части этих равенств — многочлены степени не выше 1 относительно \(x\) и \(y\):
$$
x’^<*>=A_<1>x+B_<1>y+C_<1>,\ y’^<*>=A_<2>x+B_<2>y+C_<2>.\label
$$
Подставив сюда выражения \(x\) и \(y\) по формулам \eqref, мы найдем искомую зависимость:
$$
\begin
& x’^<*>=A_<1>(\alpha_<1>x’+\beta_<1>y’+\gamma_<1>)+B_<1>(\alpha_<2>x’+\beta_<2>y’+\gamma_<2>)+C_<1>,\\
& y’^<*>=A_<2>(\alpha_<1>x’+\beta_<1>y’+\gamma_<1>)+B_<2>(\alpha_<2>x’+\beta_<2>y’+\gamma_<2>)+C_<2>.
\end\nonumber
$$
Мы видим, что правые части этих равенств — многочлены степени не выше 1 относительно \(x’\) и \(y’\). Это нам и требовалось доказать.

Заметим, что аффинные преобразования выделяются из линейных требованием взаимной однозначности, которое не зависит от системы координат. Поэтому без дополнительных проверок мы можем быть уверены, что формулы, задающие аффинное преобразование в новой системе координат, удовлетворяют условию \eqref.

Произведение линейных преобразований.

Доказательство последнего утверждения было основано на том, что результат подстановки многочленов степени не выше 1 в многочлен степени не выше 1 оказывается таким же многочленом. Это же обстоятельство лежит в основе следующего утверждения.

Произведение линейных преобразований является линейным преобразованием. Произведение аффинных преобразований — аффинное преобразование.

Пусть заданы линейные преобразования \(f\) и \(g\) и выбрана система координат. Тогда координаты точки \(f(M)\) выражаются через координаты точки \(M\) формулами
$$
x^<*>=a_<1>x+b_<1>y+c_<1>,\ y^<*>=a_<2>x+b_<2>y+c_<2>.\label
$$
а координаты точки \(g(f(M))\) через координаты точки \(f(M)\) формулами
$$
x^<**>=d_<1>x^<*>+e_<1>y^<*>+f_<1>,\ y^<**>=d_<2>x^<*>+e_<2>y^<*>+f_<2>.\label
$$
Подстановка равенств \eqref в \eqref выражает координаты g(f(M)) через координаты \(M\). В результате подстановки мы получаем многочлены степени не выше 1, что и доказывает первую часть предложения.

Для доказательства второй части достаточно вспомнить, что по согласно ранее доказанного утверждения произведение двух взаимно однозначных преобразований взаимно однозначно.

Преобразование, обратное аффинному преобразованию, также является аффинным.

Если преобразование \(f\) записано уравнениями \eqref, то координатная запись его обратного преобразования получается решением уравнений \eqref относительно \(x\) и \(y\). Для того чтобы решить эти уравнения, умножим первое из них на \(b_<2>\), второе — на \(b_<1>\) и вычтем одно уравнение из другого. Мы получим \((a_<1>b_<2>-a_<2>b_<1>)x=b_<2>(x^<*>-c_<1>)-b_<1>(y^<*>-c_<2>)\). Из условия \eqref следует, что \(x\) — линейный многочлен от \(x^<*>\) и \(y^<*>\). Выражение для \(y\) получается аналогично.

Образ вектора при линейном преобразовании.

Рассмотрим вектор \(\overrightarrowM_<2>>\). Если координаты точек \(M_<1>\) и \(M_<2>\) в системе координат \(O, \boldsymbol_<1>, \boldsymbol_<2>\) обозначить соответственно \(x_<1>, y_<1>\) и \(x_<2>, y_<2>\), то компоненты вектора будут равны \(x_<2>-x_<1>\) и \(y_<2>-y_<1>\). Пусть формулы \eqref задают преобразование \(f\) в выбранной системе координат. Тогда образы \(M_<2>^<*>\) и \(M_<1>^<*>\) точек \(M_<2>\) и \(M_<1>\) имеют абсциссы
$$
x_<2>^<*>=a_<1>x_<2>+b_<1>y_<2>+c_<1>,\ x_<1>^<*>=a_<1>x_<1>+b_<1>y_<1>+c_<1>.\nonumber
$$
Следовательно, первая компонента вектора \(\overrightarrow^<*>M_<2>^<*>>\) равна
$$
x_<2>^<*>-x_<1>^<*>=a_<2>(x_<2>-x_<1>)+b_<1>(y_<2>-y_<1>).\nonumber
$$
Аналогично находим вторую компоненту этого вектора
$$
y_<2>^<*>-y_<1>^<*>=a_<2>(x_<2>-x_<1>)+b_<2>(y_<2>-y_<1>).\nonumber
$$

Обратим внимание на то, что компоненты \(\overrightarrow^<*>M_<2>^<*>>\) выражаются только через компоненты \(\overrightarrowM_<2>>\), а не через координаты точек \(M_<1>\) и \(M_<2>\) по отдельности. Два равных вектора имеют одинаковые компоненты и, следовательно, при линейном преобразовании перейдут в векторы, компоненты которых также одинаковы. Итак, мы получаем ещё одно утверждение.

При линейном преобразовании равные векторы переходят в равные векторы. Компоненты \(\alpha_<1>^<*>\), \(\alpha_<2>^<*>\) образа вектора выражаются через его компоненты \(\alpha_<1>\), \(\alpha_<2>\) формулами
$$
\begin
& \alpha_<1>^<*>=a_<1>\alpha_<1>+b_<1>\alpha_<2>,\\
& \alpha_<2>^<*>=a_<2>\alpha_<1>+b_<2>\alpha_<2>.
\end\label
$$

Если быть точным, говорить об образе вектора при преобразовании \(f\) неправильно: преобразование отображает точки, а не векторы. Точнее было бы сказать, что \(f\) порождает преобразование \(\tilde\) множества векторов. Но ниже мы, тем не менее, будем придерживаться не совсем точной, но более удобной и общепринятой терминологии — говорить, что преобразование \(f\) переводит вектор \(\boldsymbol\) в вектор \(\boldsymbol^<*>\) и обозначать последний через \(f(\boldsymbol)\).

Из равенств \eqref следует, что при линейном преобразовании \(f\) линейно зависимые векторы переходят в линейно зависимые. Действительно, как легко видеть, \(f(\boldsymbol<0>)=\boldsymbol<0>\). Тогда любое соотношение вида \(\lambda \boldsymbol+\mu \boldsymbol=\boldsymbol<0>\) влечет за собой \(\lambda f(\boldsymbol)+\mu f(\boldsymbol)=\boldsymbol<0>\).

Следующее утверждение устанавливает геометрический смысл коэффициентов в формулах, задающих линейное преобразование.

Пусть преобразование \(f\) записано в системе координат \(O, \boldsymbol_<1>, \boldsymbol_<2>\) формулами \eqref. Тогда \(c_<1>\) и \(c_<2>\) — координаты точки \(f(O)\), a \(a_ <1>a_<2>\) и \(b_<1>, b_<2>\) — компоненты векторов \(f(\boldsymbol_<1>)\) и \(f(\boldsymbol_<2>)\) в системе координат \(O, \boldsymbol_<1>, \boldsymbol_<2>\).

Для доказательства подставим в формулы \eqref значения \(x=0\) и \(y=0\) координат точки \(O\) и увидим, что координаты \(f(O)\) равны \(c_<1>\) и \(c_<2>\).

Подставим в формулы \eqref координаты вектора \(\boldsymbol_<1>\) \(\alpha_<1>=1\), \(\alpha_<2>=0\) и найдем \(a_<1>^<*>=a_<1>\), \(a_<2>^<*>=a_<2>\). Следовательно, \(f(\boldsymbol_<1>)\) имеет компоненты \(a_<1>\) и \(a_<2>\). Так же доказывается, что компоненты \(f(\boldsymbol_<2>)\) равны \(b_<1>\) и \(b_<2>\).

Каковы бы ни были три точки \(L\), \(M\), \(N\), не лежащие на одной прямой, и три точки \(L^<*>\), \(M^<*>\) и \(N^<*>\), существует единственное линейное преобразование \(f\) такое, что \(L^<*>=f(L)\), \(M^<*>=f(M)\) и \(N^<*>=f(N)\). Это преобразование аффинное тогда и только тогда, когда точки \(L^<*>\), \(M^<*>\) и \(N^<*>\) также не лежат на одной прямой.

Векторы \(\overrightarrow\) и \(\overrightarrow\) не коллинеарны. Следовательно, \(L\), \(\overrightarrow\), \(\overrightarrow\) — декартова система координат. Пусть \(c_<1>, c_<2>\) — координаты \(L^<*>\), а \(a_<1>, a_<2>\) и \(b_<1>, b_<2>\) — компоненты векторов \(\overrightarrowM^<*>>\) и \(\overrightarrowN^<*>>\) в этой системе координат. Формулы
$$
x^<*>=a_<1>x+b_<1>y+c_<1>,\ y^<*>=a_<2>x+b_<2>y+c_<2>\nonumber
$$
определяют линейное преобразование \(f\), которое, как легко видеть, обладает требуемым свойством. При этом согласно предложению 7, коэффициенты в формулах однозначно определены.

Условие \eqref, равносильное аффинности преобразования, необходимо и достаточно для того, чтобы векторы \(\overrightarrowM^<*>>\) и \(\overrightarrowN^<*>>\) были не коллинеарны, то есть \(L^<*>\), \(M^<*>\) и \(N^<*>\) не лежали на одной прямой. Предложение доказано.

Заметим, что в том случае, когда преобразование \(f\) аффинное, точка \(f(O)\) и векторы \(f(\boldsymbol_<1>)\) и \(f(\boldsymbol_<2>)\) могут быть использованы как система координат. Для этой системы координат имеет место ещё одно утверждение.

При аффинном преобразовании \(f\) образ \(M^<*>\) точки \(M\) в системе координат \(f(O)\), \(f(\boldsymbol_<1>)\), \(f(\boldsymbol_<2>)\) имеет те же координаты, что и точка \(M\) в системе координат \(O, \boldsymbol_<1>, \boldsymbol_<2>\).

Равенство \(\overrightarrow=x \boldsymbol_<1>+y \boldsymbol_<2>\) означает, что \(x\), \(y\) — координаты \(M\) в системе координат \(O, \boldsymbol_<1>, \boldsymbol_<2>\). Подействовав преобразованием \(f\) на обе части этого равенства, мы получаем \(\overrightarrow=x f(\boldsymbol_<1>)+y f(\boldsymbol_<2>)\), которое означает, что \(x\) и \(y\) — координаты \(M^<*>\) в системе координат \(f(O)\), \(f(\boldsymbol_<1>)\), \(f(\boldsymbol_<2>)\).

Источник

Линейное преобразование

Лине́йным отображе́нием (лине́йным опера́тором) векторного пространства L_K над полем K в векторное пространство M_K (над тем же полем K ) называется отображение

,

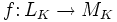
удовлетворяющее условию линейности

для всех и .

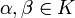
Содержание

Важные частные случаи

Связанные понятия

Примеры

Примеры линейных однородных операторов:

Примеры линейных неоднородных операторов:

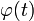
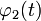
где , , — вполне определённые функции, а x(t) — преобразуемая оператором функция.

См. также

Полезное

Смотреть что такое «Линейное преобразование» в других словарях:

линейное преобразование — [IEV number 314 02 04] EN linear conversion conversion for which the quotient of each change in the output value by the corresponding change in the input value is intended to be constant [IEV number 314 02 04] FR conversion linéaire… … Справочник технического переводчика

Линейное преобразование — Л., или проективным, преобразованием плоскости называется такой переход от одной плоскости к другой, при котором все точки любой прямой, лежащей в первой плоскости, образуют во второй плоскости тоже прямую. Этот переход достигается… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

линейное преобразование — tiesinė transformacija statusas T sritis automatika atitikmenys: angl. linear transformation vok. Lineartransformation, f rus. линейное преобразование, n pranc. transformation linéaire, f … Automatikos terminų žodynas

линейное преобразование — tiesinis keitimas statusas T sritis Standartizacija ir metrologija apibrėžtis Keitimas, kai išėjimo dydžio kiekvienos vertės ir atitinkamos įėjimo dydžio vertės pokyčių dalmuo yra pastovus. atitikmenys: angl. linear conversion vok. linear… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

линейное преобразование — tiesinė transformacija statusas T sritis fizika atitikmenys: angl. linear transformation vok. lineare Transformation, f rus. линейное преобразование, n pranc. transformation linéaire, f … Fizikos terminų žodynas

ЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ — отображение векторного пространства в себя, при к ром образом суммы двух векторов является сумма их образов, а образом произведения вектора на число произведение образа вектора на это число. Если V векторное пространство, f заданное в нем Л. п. и … Математическая энциклопедия

Источник

Линейные преобразования: свойства, для чего они нужны, типы, примеры

Содержание:

А линейное преобразование, который мы будем просто называть T, связывает элементы двух векторных пространств V и W, присваивая каждому вектору v принадлежащий V один вектор ш который принадлежит W, посредством определенной операции.

Это преобразование соответствует двум условиям:

-Условие 1

Это относится к сложению, чтобы преобразование T было линейным, должно быть верно, что:

Т (v + ш) = Т (v) + Т (ш)

-Условие 2

Второе условие представляет собой однородность умножения скаляра на вектор:

Т (сv) = c⋅T (v)

Линейное преобразование, как следует из названия, отвечает за отображение или преобразование элементов V в элементы W.

Пример линейного преобразования:

Если у нас есть вектор:

Преобразование возвращает нас:

Свойства линейных преобразований

Предположим линейное преобразование T из V в W, в котором векторы v Y или принадлежат V, то верны следующие свойства:

Свойство 1

Т (0) = 0

Свойство 2

Свойство 3

Свойство 4

Быть v = c₁v₁ + c₂v₂ +…. + c_пv_п

Элементы линейного преобразования

–Ядро T или ядро: является подмножеством области, обозначаемой N (Т) или ker (T) и включает в себя все элементы V такие, что:

Т (v) = 0.

Линейное преобразование T (v) = 0 называется нулевое преобразование.

Естественно нулевой вектор v = 0 он в любом случае удовлетворяет этому условию, но ядро ​​состоит из набора ненулевых векторов, которые также удовлетворяют этому условию для данного T.

Эти элементы помогут нам позже классифицировать линейные преобразования.

Для чего нужны линейные преобразования?

Первоначально линейные преобразования работают с векторными пространствами, состоящими из векторов. Мы часто связываем векторы с силами и другими физическими величинами, однако при цифровой обработке изображений пиксель может быть представлен вектором.

В этом случае изображением можно управлять с помощью удобных линейных преобразований для получения желаемых эффектов, например проецирования, поворота, поиска зеркального изображения или изменения его размера без изменения относительных размеров.

Линейные преобразования также широко используются в экономике и принятии решений, например, для определения количества сырья, необходимого для производства определенной партии продукции.

Как мы увидим позже, количество деталей, необходимых для сборки различных моделей, производимых фабрикой, можно определить с помощью матричной схемы.

Типы линейных преобразований (классификация)

Как и функции, линейные преобразования могут быть:

-Инъективы или мономорфизмы

-Цели или эпиморфизмы

-Overjectives или изоморфизмы

Также существуют следующие виды:

Инъективные линейные преобразования

Ker (T) = 0

Сюръективные линейные преобразования

Биективные линейные преобразования

Линейное преобразование T: V → W биективно, если оно одновременно инъективно и сюръективно. Следовательно, верно, что:

Ker (T) = 0 а также Im (T) = W

Эндоморфизмы

Это линейные преобразования, в которых область и область значений совпадают.

Автоморфизмы

Специальные линейные преобразования

Линейный оператор

Линейное преобразование T: V → V, которое переходит из векторного пространства в то же векторное пространство, называется линейный оператор.

Нулевое преобразование

Упомянутое выше нулевое преобразование важно для нахождения ядра линейного преобразования:

T: V → W такое, что T (v) = 0 Для любой v.

Трансформация идентичности

T: V → V такое, что T (v) = v Для любой v.

Преобразование, определяемое матрицей

Линейная функция

Линейные функции типа y = mx являются линейными преобразованиями. Возьмите, например, y = 3x и посмотрите, удовлетворяет ли он двум условиям в начале, проверяя с любыми двумя значениями a и b:

f (a + b) = 3 (a + b) = 3a + 3b = f (a) + f (b)

f (ka) = 3 (ka) = k⋅ (3a) = k⋅f (a)

По сути, это линейное преобразование.

Приложения

У линейных преобразований есть математические приложения, такие как:

-Вращение координатных осей.

-При решении систем линейных дифференциальных уравнений.

-Задачи собственных значений и собственных векторов.

И у них также есть приложения в других областях науки, например, в механике, квантовой механике и экономике, среди других областей.

Примеры линейных преобразований

Пример 1

Во многих задачах механики нам нужно найти проекцию вектора v принадлежащий пространству, на определенной плоскости. Этот вектор v он может представлять, например, силу.

Предположим, вы хотите спроецировать вектор v = на плоскости xy. Мы можем определить линейное преобразование, задаваемое следующей матрицей:

Когда мы применяем его к вектору v получаем вектор, z-компонента которого равна нулю. Геометрически он представлен так, с проекцией v на плоскости xy как двухкомпонентный красный вектор.

Пример 2

Предположим, у вас есть фабрика, которая производит три типа игрушечных машинок: C1, C2 и C3, для которых вам нужно три типа деталей в определенных количествах для изготовления каждого типа тележки:

-Колеса или деталь B

Для каждого типа тележки количество штук разное, так как модели разные. Мы можем упорядочить количество в матрице 3 × 3, в которой столбцы возглавляются типом тележки, а строки соответствуют количеству штук, необходимых для изготовления каждой модели.

Это пример преобразования матрицы, которая будет выглядеть так:

Если фабрика получает определенный заказ на поставку, который состоит из Икс количество C1, Y из C2 и z Из C3, сколько деталей A, B и C вам нужно иметь в наличии для сборки тележек для заказов?

Мы должны найти такое линейное преобразование T (x), что:

Чтобы получить вектор Y:

Это даст нам необходимое количество деталей. В решенном упражнении 2 мы оценили эффективность линейных преобразований, чтобы найти количество деталей, необходимых для выполнения определенного заказа.

Решенные упражнения

— Упражнение 1

Убедитесь, что следующее преобразование T: R 2 → R 2 линейно:

Решение

Первое условие

-Поминая, что векторы добавляются компонент за компонентом, необходимо убедиться, что:

Т (v+или) = Т (v) + Т (или)

Т (v+или) = T (x₁+ х₂ ; Y₁ + и₂)

Отсюда получается, что:

-С другой стороны, при применении преобразования к каждому вектору отдельно:

Сложив полученные векторы, мы фактически получаем:

Поскольку оба результата идентичны, первое условие выполнено.

Второе условие

Теперь мы собираемся проверить, что при умножении на скаляр c это можно не учитывать при преобразовании:

Т (сv) = c⋅T (v)

Таким образом, поскольку оба выражения идентичны, второе условие также выполняется и преобразование является линейным.

— Упражнение 2.

Завод игрушечных автомобилей собирает три модели автомобилей: C1, C2 и C3, для которых ему нужны детали A, B и C, которые являются соответственно осями, колесами и шасси. Необходимые количества указаны в следующей таблице:

Завод попросили построить 12 моделей C1, 22 C2 и 16 C3. Сколько деталей A, B и C необходимо для выполнения заказа?

Решение

Применяется линейное преобразование T (x) = Y, результатом которого является произведение матриц:

Всего они необходимы:

Ссылки

Интервью с Фернандо Каллехо: психология в помощь музыкантам

Семена стервятника: для чего они нужны, побочные эффекты

Источник