можно ли утверждать что несобственный интеграл относится к определенному интегралу

2.1. Понятие несобственного интеграла

Это «родственник» определённого интеграла. …Нормальное такое определение :). И сразу возникает вопрос: чем отличается несобственный интеграл от «собрата»? Он может отличаться пределами интегрирования:
– то есть, один или даже оба предела бесконечны, при этом подынтегральная функция непрерывна на промежутке интегрирования.

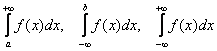
Такие интегралы получили название несобственные интегралы первого рода.

Кроме того, несобственный интеграл может быть «внешне похож» на определённый интеграл и иметь вид 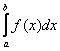. Но есть один нюанс. Подынтегральная функция не определена в точке или . Или на обоих концах. Или даже во внутренних точках отрезка .

Это так называемые несобственные интегралы второго рода.

Что значит решить несобственный интеграл? В отличие от определённого интеграла, тут есть три варианта. Решить несобственный интеграл – это значит найти конечное число, либо получить бесконечность, либо выяснить, что несобственного интеграла не существует.

1) Если несобственный интеграл равен конечному числу, то говорят, что он сходится. Число может быть как положительным, так и отрицательным. Или нулём.

2) Если несобственный интеграл равен бесконечности (со знаком «плюс» или «минус»), то говорят, он расходится.

3) И в ряде случаев несобственного интеграла может вовсе не существовать. Даже если подынтегральная функция непрерывна на промежутке интегрирования! (вспоминаем, что определённый интеграл при этом условии существует всегда).

Как решить несобственный интеграл? С помощью той же формулы Ньютона-Лейбница. С некоторыми особенностями.

И здесь вы должны понимать и уметь решать несложные пределы функций.

В чём смысл несобственного интеграла? Геометрически – это тоже площадь (если интеграл существует). Но площадь своеобразная. И с этим своеобразием мы познакомимся прямо на следующей странице:

Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!

С наилучшими пожеланиями, Александр Емелин

Источник

Несобственные интегралы

Определение несобственных интегралов.

Интеграл Римана был введен для ограниченных на отрезке функций. Естественно поставить вопрос о распространении понятия интеграла на случай бесконечного промежутка, а также на случай, когда подынтегральная функция является неограниченной.

Интеграл на бесконечном промежутке.

Рассмотрим функцию \(\displaystyle\frac<1><1+x^<2>>\). Эта функция непрерывна на отрезке \([0,\xi]\) при любом \(\xi \geq 0\), и поэтому существует интеграл \(J(\xi) = \displaystyle\int\limits_0^ <\xi>\frac<1+x^<2>> = \operatorname \xi\), откуда следует, что \(\displaystyle\lim_ <\xi \rightarrow \infty>J(\xi) = \frac<\pi><2>\). В этом случае пишут \(\displaystyle\int\limits_0^ <+\infty>\frac<1+x^<2>> = \frac<\pi><2>\), а символ \(\displaystyle\int\limits_0^ <+\infty>\frac<1+x^<2>>\) называют несобственным интегралом от функции \(\displaystyle\frac<1><1+x^<2>>\) на бесконечном промежутке \([0, +\infty)\).

Число \(\displaystyle\frac<\pi><2>\) — можно интерпретировать как площадь фигуры, ограниченной графиком функции \(y = \displaystyle\frac<1><1+x^<2>>,\ x \geq 0\), и координатными осями (рис. 38.1).

Рис. 38.1

Рассмотрим несобственный интеграл на бесконечном промежутке от функции \(f\).

Пусть функция \(f(x)\) определена при \(x \geq a\), где \(a\) — заданное число, и интегрируема на отрезке \([a,\xi]\) при любом \(\xi \geq a\). Тогда символ \(\displaystyle\int\limits_a^ <+\infty>f(x)\ dx\) будем называть несобственным интегралом от функции \(f\) на промежутке \([0, +\infty)\). Если существует конечный \(\displaystyle\lim_ <\xi \rightarrow +\infty>\int\limits_a^ <+\infty>f(x)\ dx = A\), то говорят, что несобственный интеграл \(\displaystyle\int\limits_a^ <+\infty>f(x)\ dx\) сходится и равен \(A\), а функцию \(f\) называют интегрируемой в несобственном смысле на промежутке \([a, +\infty)\). Таким образом, сходящийся несобственный интеграл от функции \(f\) на промежутке \([a, +\infty)\) определяется равенством
$$
\int\limits_a^ <+\infty>f(x)\ dx = \lim_ <\xi \rightarrow +\infty>\int\limits_a^ <\xi>f(x)\ dx.\label
$$

Если функция \(\displaystyle\int\limits_a^ <\xi>f(x)\ dx\) не имеет конечного предела при \(\xi \rightarrow +\infty\), то говорят, что несобственный интеграл \(\displaystyle\int\limits_a^ <+\infty>f(x)\ dx\) расходится.

Сходимость интеграла \eqref равносильна сходимости интеграла \(\displaystyle\int\limits_c^ <+\infty>f(x)\ dx\), где \(c\) — любое число из промежутка \((a, +\infty)\), так как
$$
\int\limits_a^ <\xi>f(x)\ dx = \int\limits_a^c f(x)\ dx+\int\limits_c^ <\xi>f(x)\ dx.\nonumber
$$

Показать, что интеграл \(J = \displaystyle\int\limits_<-\infty>^0 xe^<-x^<2>>\ dx\) сходится, и вычислить этот интеграл.

Показать, что интеграл \(J = \int\limits_<-\infty>^ <+\infty>\frac<1+x+x^<2>>\) сходится, и вычислить этот интеграл.

Исследовать на сходимость интеграл
$$
J(\alpha) = \int\limits_1^ <+\infty>\frac>.\label
$$

Интеграл на конечном промежутке.

Рис. 38.2

Обратимся к несобственному интегралу на конечном промежутке.

Пусть функция \(f(x)\) определена на конечном промежутке \([a, b)\), интегрируема на отрезке \([a, \xi]\) при любом \(\xi \in [a, b)\).

Если существует конечный \(\displaystyle\lim_ <\xi \rightarrow b-0>\int\limits_a^ <\xi>f(x)\ dx = A\), то говорят, что несобственный интеграл от функции \(f(x)\) на промежутке \([a, b)\) равен \(A\). Его обозначают символом \(\displaystyle\int\limits_a^b f(x)\ dx\). Таким образом, по определению
$$
\int\limits_a^b f(x)\ dx = \lim_ <\xi \rightarrow b-0>\int\limits_a^ <\xi>f(x)\ dx.\label
$$

В случае существования конечного предела \eqref несобственный интеграл \(\displaystyle\int\limits_a^b f(x)\ dx\) называют сходящимся, в противном случае — расходящимся; символ \(\int\limits_a^b f(x)\ dx\) употребляют как в случае сходимости, так и в случае расходимости интеграла.

Аналогично, если функция \(f(x)\) определена на конечном промежутке \((a, b]\), интегрируема на отрезке \([\xi, b]\) при любом \(\xi \in (a, b]\), то символ \(\displaystyle\int\limits_a^b f(x)\ dx\) называют несобственным интегралом от функции \(f\) на промежутке \((a, b]\).

Если существует конечный \(\displaystyle\lim_ <\xi \rightarrow a+0>\int\limits_<\xi>^b f(x)\ dx = A\), то говорят, что несобственный интеграл сходится и равен \(A\), то есть
$$
\int\limits_a^b f(x)\ dx = \lim_ <\xi \rightarrow a+0>\int\limits_<\xi>^b f(x)\ dx.\label
$$

Если функция \(\displaystyle\int\limits_<\xi>^b f(x)\ dx\) не имеет конечного предела при \(\xi \rightarrow a+0\), то несобственный интеграл называют расходящимся.

Определение \eqref несобственного интеграла на конечном промежутке \([a, b)\) является содержательным лишь в случае, когда функция \(f\) неограничена на интервале \((b-\delta, b)\) при любом \(\delta > 0\). В самом деле, если функция \(f\) интегрируема на отрезке \([a, \xi]\) при любом \(\xi \in [a, b)\) и ограничена на \([a, b)\), то, доопределив эту функцию в точке \(b\), получим функцию, которая интегрируема по Риману на отрезке \([a, b]\). При этом интеграл от доопределенной функции равен пределу \eqref и не зависит от значения функции в точке \(b\).

Поэтому в дальнейшем, рассматривая несобственный интеграл \eqref, будем считать, что функция \(f\) является неограниченной на интервале \((b-\delta, b)\) при любом \(\delta > 0\), а точку \(b\) будем называть иногда особой точкой подынтегральной функции \(f\) или интеграла \eqref.

Аналогично, рассматривая несобственный интеграл \eqref, будем считать, что \(a\) — особая точка функции \(f\), то есть предполагать, что функция \(f\) неограничена на интервале \((a, a+\delta)\) при любом \(\delta > 0\).

Исследовать на сходимость интеграл
$$
J = \int\limits_0^1 \frac>.\nonumber
$$

\(\vartriangle\) Обозначим \(F(\xi) = \displaystyle\int\limits_<\xi>^ <1>\frac>\), тогда
$$
F(\xi) = \left\<\begin
\frac<1><1-\alpha>(1-\xi^<1-\alpha>),\ \mbox<если>\ \alpha \neq 1 \\
-\ln \xi,\ \mbox<если>\ \alpha = 1.
\end \right.\nonumber
$$
Поэтому при \(\alpha Замечание 3.

Сходимость несобственного интеграла \eqref равносильна сходимости интеграла \(\displaystyle\int\limits_c^b f(x)\ dx\) при любом \(c \in (a, b)\), так как \(\displaystyle\int\limits_a^ <\xi>f(x)\ dx = \int\limits_a^c f(x)\ dx+\int\limits_c^ <\xi>f(x)\ dx\).

Другие типы несобственных интегралов.

Если функция \(f\) определена на конечном интервале \((a, b)\), интегрируема по Риману на отрезке \([\xi, \eta]\) при любых \(\xi,\ \eta\) таких, что \(a

Свойства и вычисление несобственных интегралов.

Будем рассматривать несобственные интегралы вида \(\displaystyle\int\limits_a^b f(x)\ dx\) предполагая, что:

Согласно определению сходящегося несобственного интеграла
$$
\int\limits_a^b f(x)\ dx = \lim_ <\xi \rightarrow b-0>\int\limits_a^ <\xi>f(x)\ dx,\ \mbox<если>\ b \neq +\infty,\nonumber
$$
$$
\int\limits_a^ <+\infty>f(x)\ dx = \lim_ <\xi \rightarrow +\infty>\int\limits_a^ <\xi>f(x)\ dx\ \mbox<если>\ b = +\infty.\nonumber
$$

Линейность интеграла.

Если сходятся несобственные интегралы от функций \(f(x)\) и \(g(x)\) на промежутке \([a, b)\), то при любых \(\lambda, \mu \in \mathbb\) сходится интеграл от функции \(\lambda f(x)+\mu g(x)\) на том же промежутке и выполняется равенство
$$
\int\limits_a^ <\xi>(\lambda f(x)+\mu g(x))\ dx = \lambda \int\limits_a^ <\xi>f(x)\ dx+\mu \int\limits_a^ <\xi>f(x)\ dx,\label
$$

\(\circ\) Для любого \(\xi \in [a, b)\) в силу свойств интеграла Римана справедливо равенство
$$
\int\limits_a^ <\xi>(\lambda f(x)+\mu g(x))\ dx = \lambda \int\limits_a^ <\xi>f(x)\ dx+\mu \int\limits_a^ <\xi>f(x)\ dx,\nonumber
$$
правая часть которого имеет по условию конечный предел при \(\xi \rightarrow b-0\), откуда следует существование предела при \(\xi \rightarrow b-0\) в левой части и справедливость формулы \eqref. \(\bullet\)

Формула Ньютона-Лейбница.

Если функция \(f(x)\) непрерывна на промежутке \([a, b)\) и если \(F(x)\) — первообразная для функции \(f(x)\), то несобственный интеграл \(\displaystyle\int\limits_a^b f(x)\ dx\) сходится тогда и только тогда, когда существует конечный
$$
\lim_ <\xi \rightarrow b-0>F(\xi) = F(b-0),\label
$$
причем
$$
\int\limits_a^b f(x)\ dx = F(b-0)-F(a).\label
$$

\(\circ\) Так как функция \(f\) непрерывна на отрезке \([a, \xi]\) при любом \(\xi \in [a, b)\), то справедлива формула Ньютона-Лейбница
$$
\int\limits_a^ <\xi>f(x)\ dx = F(\xi)-F(a),\nonumber
$$
откуда, переходя к пределу при \(\xi \rightarrow b-0\) и используя соотношение \eqref, получаем формулу \eqref, которую называют формулой Ньютона Лейбница для несобственного интеграла.
Правую часть формулы \eqref часто записывают в виде \(\displaystyle\left.F(x)\right|_^\), если \(b \neq +\infty\). Если \(b = +\infty\), то правую часть формулы \eqref записывают в виде \(\displaystyle\left.F(x)\right|_^<+\infty>\). \(\bullet\)

Интегрирование по частям.

Пусть функции \(u(x)\), \(v(x)\) определены на промежутке \([a, b)\), имеют непрерывные производные на отрезке \([a, \xi]\) для любого \(\xi \in (a, b)\). Если существует конечный предел
$$
\lim_ <\xi \rightarrow b-0>[u(\xi)v(\xi)] = u(b-0)v(b-0) = uv|_<\xi = b-0>,\label
$$
и интеграл \(\displaystyle\int\limits_a^b vu’\ dx\) сходится, то и интеграл \(\displaystyle\int\limits_a^b uv’\ dx\) сходится и справедлива формула интегрирования по частям
$$
\int\limits_a^b uv’\ dx = uv|_^-\int\limits_a^b vu’\ dx.\label
$$

\(\circ\)Так как функции \(u'(x)\), \(v'(x)\) непрерывны на отрезке \([a, \xi]\) при любом \(\xi \in (a, b)\), то справедлива формула интегрирования по частям
$$
\int\limits_a^ <\xi>uv’\ dx = u(\xi)v(\xi)-u(a)v(a)-\int\limits_a^ <\xi>vu’\ dx.\label
$$
Правая часть равенства \eqref по условию имеет при \(\xi \rightarrow b-0\) конечный предел, равный правой части формулы \eqref. Следовательно, существует конечный предел и в левой части \eqref, то есть сходится интеграл \(\displaystyle\int\limits_a^b uv’\ dx\), и при этом справедлива формула \eqref.

Отметим, что при наличии конечного предела \eqref несобственные интегралы \(\displaystyle\int\limits_a^b vu’\ dx\) и \(\displaystyle\int\limits_a^b uv’\ dx\) сходятся или расходятся одновременно. \(\bullet\)

Вычислить несобственный интеграл \(J = \displaystyle\int\limits_0^ <+\infty>xe^<-x>\ dx\).

Замена переменного.

Если функция \(f(x)\) непрерывна на промежутке \([a, b)\), а функция \(x = \varphi(t)\) непрерывно дифференцируема на промежутке \([\alpha, \beta)\), строго возрастает и удовлетворяет условиям \(\displaystyle\varphi(\alpha) = a,\ \lim_\varphi(t) = b\), то справедлива формула замены переменного
$$
\int\limits_a^b f(x)\ dx = \int\limits_<\alpha>^ <\beta>f(\varphi(t))\varphi'(t)\ dt.\label
$$
при условии, что хотя бы один из интегралов в \eqref сходится.

\(\circ\) Пусть \(\tau \in [\alpha, \beta),\ \varphi(\tau) = \xi\). Тогда \(\varphi(\tau) \rightarrow b\) при \(\tau \rightarrow \beta-0\). Применяя формулу замены переменного для интеграла Римана, получаем
$$
\int\limits_a^ <\xi>f(x)\ dx = \int\limits_<\alpha>^ <\tau>f(\varphi(t))\varphi'(t)\ dt.\label
$$
Так как функция \(x = \varphi(t)\) строго возрастает и непрерывна на \([\alpha, \beta)\), то обратная функция строго возрастает и непрерывна на \([a, b)\). Поэтому если существует конечный предел при \(\tau \rightarrow \beta-0\) правой части равенства \eqref, то существует конечный предел при \(\xi \rightarrow b\) в левой части (и наоборот), и при этом справедлива формула \eqref. \(\bullet\)

Вычислить интеграл \(J = \displaystyle\int\limits_0^ <+\infty>\frac<(x^<2>+1)^<3>>\).

\(\vartriangle\) Положим \(x = \operatorname t\), где \(0 Пример 8.

Вычислить интеграл \(J = \displaystyle\int\limits_0^ <+\infty>\frac+1><(x^<4>+1)>\ dx\).

\(\vartriangle\) Преобразуем интеграл \(J = \displaystyle\int\limits_0^ <+\infty>\frac<(1+1/x^<2>)dx><(x-1/x)^<2>+2>\ dx\) и положим \(\displaystyle x-\frac<1> = t\); тогда
$$
J = \int\limits_<-\infty>^<+\infty>\frac